Excel MINVERSE Function: Inverse Matrix

by

In this article, you will learn how to calculate inverse of a matrix and the usage of MINVERSE function in Excel.

The inverse of a matrix refers to a matrix that when multiplied by original matrix gives the identity matrix. Calculating the inverse of a matrix is a fundamental concept in linear algebra, often used in various applications such as solving systems of equations, and data analysis. In Excel, the MINVERSE function simplifies this process, allowing users to quickly calculate the inverse of a matrix.

MINVERSE function

Excel MINVERSE function calculates the inverse of an nxn square matrix. After typing the function, select the cell range where you define elements of the matrix. MINVERSE function is available in Excel 2003 and later versions.

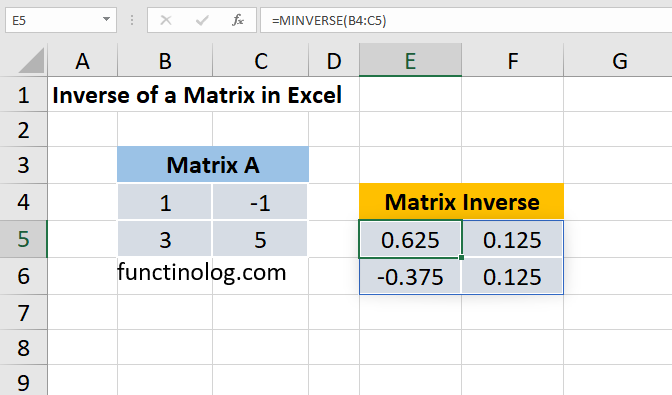
excel minverse function

The following formula calculates the inverse of 2×2 square matrix in the cell range B4:C5.

=MINVERSE (B4:C5)

MINVERSE returns the #VALUE! error value if the matrix does not have an equal number of rows and columns (non-square).

Inverse of a Matrix Example

First, let’s enter a 3×3 matrix A in any cell range in Excel worksheet. In the example below, we have entered the matrix A in cell range B4:D6. After that, let’s select the cell (B9) where we want to place the result and type the formula.

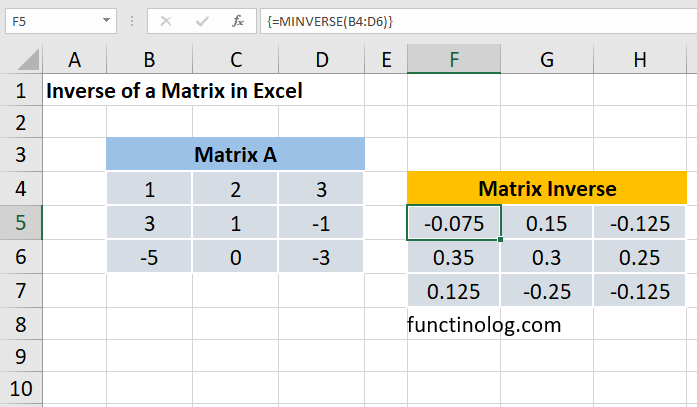
inverse matrix in excel

In order to get the inverse of a matrix, we use MINVERSE function, which is a built-in function in Excel. After typing the function, select B4:D6 cell range as follows.

=MINVERSE (B4:D6)

However, you do not press enter. Use CTRL + Shift and Enter keys. You will see curly brackets in the formula. If you don’t use this shortcut and press enter directly, you will get an error message. The formula will be as follows.

{=MINVERSE (B4:D6)}

If you have Microsoft 365 version, you don’t need to use this key combination. After typing the formula, just press enter. The spill feature calculates the formula for all cells.

You can repeat the above steps to find the inverse of matrices with different dimensions.

When calculating the inverse of a square matrix If you get a #NUM! error, it means that the matrix cannot be inverted. You can test whether it is invertible by calculating the determinant of the matrix. If the determinant of the matrix is non-zero, it is invertible. To calculate the determinant, you can check out the last part of the page.

Non-square matrix inversion (Pseudo-Inverse)

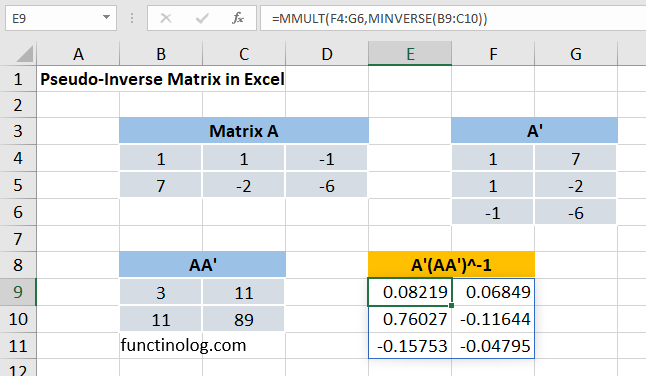
We can directly use MINVERSE function for square matrices. However, non-square matrices do not have an inverse. We can calculate the inverse of the mxn dimensional matrix using pseudo-inverse (Moore–Penrose inverse).

Let’s consider a matrix A (size of mxn). If n > m then matrix A has a right inverse matrix. Thus, pseudo inverse is calculated with the expression (AT A)-1 AT . If n<m, matrix A has left inverse matrix and its pseudo inverse is calculated as A (AAT )-1 .

non-square (pseudo inverse) matrix in excel

Key points for using MINVERSE

  • Array Formula: MINVERSE must be entered as an array formula by pressing Ctrl + Shift + Enter, except in Microsoft 365.
  • #VALUE error: Occurs if the matrix contains non-numerical values, is not square, or has empty cells.
  • #N/A error: Happens when the inverse matrix extends beyond the selected range.
  • #NUM error: Appears when the matrix is singular (determinant is zero).
  • Verifying Results: Multiply the original matrix by its inverse. If the result is an identity matrix, your inverse is correct.