In this article, you’ll learn how to solve quadratic equations and practice in Excel.
A quadratic equation is a type of polynomial equation of the second degree. The general form of a quadratic equation is ax2 + bx + c = 0. In this equation, “a”, “b”, and “c” are coefficients. “x” represents the variable we want to solve for. “x2” represents the squared term, “bx” is the linear term, and “c” is the constant.
How to solve quadratic equations in Excel
Before starting to solve a quadratic equation in Excel, let’s talk about the mathematical expressions of this operation. The quadratic formula below is a commonly used method to find the roots of a quadratic equation:
x = (-b ± √(b² – 4ac)) / (2a)
The value inside the square root, “b² – 4ac” is called the discriminant. The solution of the quadratic equation depends on the value of the discriminant:
- If the discriminant is positive (b² – 4ac > 0), there are two distinct real roots.
- If the discriminant is zero (b² – 4ac = 0), there is one real solution (a repeated root).
- If the discriminant is negative (b² – 4ac < 0), there are no real solution, but there are complex roots.
To solve a quadratic equation in Excel, let’s see an example now.
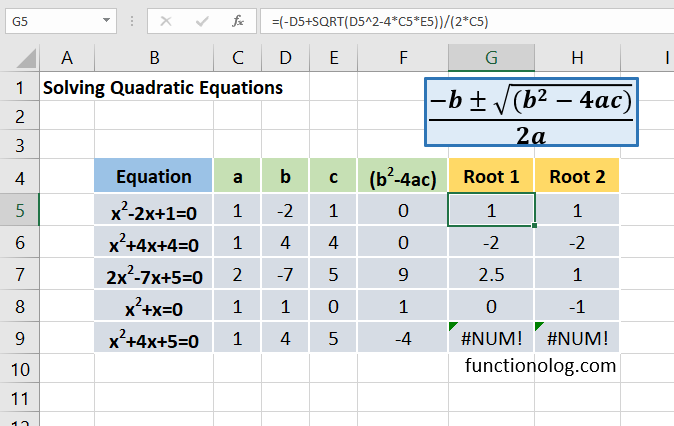
For instance, to solve an equation like x2-2x+1=0, type the coefficients to the cells C5, D5,and E5 respectively. To check the discriminant value type the formula =D5^2-4*C5*E5 to the cell F5. Finally, the formula below in the cell G5 returns the first real root.
=(-D5+SQRT(D5^2-4*C5*E5))/(2*C5)
And the second root is calculated by the formula in the cell H5.
=(-D5-SQRT(D5^2-4*C5*E5))/(2*C5)
Finding complex roots of quadratic equation
We know that a quadratic equation has complex roots if the discriminant (b² – 4ac) is less than zero. To calculate the complex roots of a quadratic equation, we’ll need some functions other than those used in calculating real roots. These are built-in complex Excel functions: IMDIV, IMSUM.
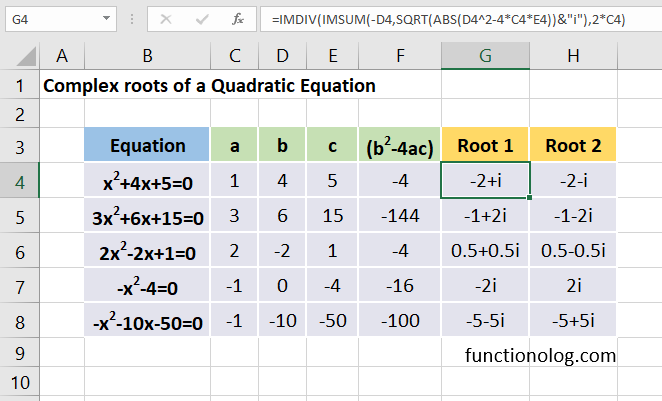
The formula in the cell G4 returns the first complex root of the equation.
=IMDIV(IMSUM(-D4,SQRT(ABS(D4^2-4*C4*E4))&”i”),2*C4)
The second one in the cell H4 is as follows:
=IMDIV(IMSUM(-D4,-SQRT(ABS(D4^2-4*C4*E4))&”i”),2*C4)